Voronoi and Delaunay

Do you know what Voronoi Diagrams and Delaunay Triangulations are? I did not until a few weeks ago.

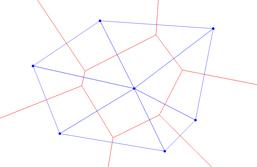
Basically a Voronoi diagram is a set of convex polygons, like in the image to the right. They are created from a set of points called seeds. All of the points within each polygon are closer to that polygon’s seed than to any of the other polygon's seeds. The points along an edge are the same distance to the seed points of those two polygons. The point at each vertex is the same distance from at least three seed points.

Still with me?

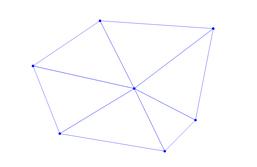
The Delaunay triangulation is a set of triangles connecting the seed points of each polygon to its two nearest neighboring seed points.

So what good are they?

There are a lot of uses for them. If each seed point was an obstacle to avoid then a self-driving car could use the edges of the Delaunay triangulation to find the safest path through the obstacles. John Snow created a Voronoi diagram of London showing that cholera deaths of 1854 were closer to one water pump than to the others. You could even draw a Voronoi diagram on a map using coffee shops as the seed points, so you would always know which one you were nearest to. There are many applications in many fields, like chemistry, biology, astronomy, mathematics, 3D graphics, telecommunications and so forth.

Of course you want to draw one by hand, so here is how:
Start off with some random points on your paper. These are your seed points. The more points you add the more complex the diagram becomes the more time it takes to draw.

Make the Delaunay Triangulation by connecting the points.

Find the middle point on each side of the triangles. Draw a line perpendicular to each side at that midpoint. These lines become the sides of the polygons and the points where they intersect are the vertices of the polygons. Below, the blue lines are the Delaunay Triangulation and the red are the Voronoi Diagram.